You could say that the research of mathematics student Lisa Piccirillo (Ph.D. ’19) is from another dimension: it examines the topology and geometry of four-dimensional spaces.
Piccirillo’s dissertation “Knot Traces and the Slice Genus,” is the winner of the 2019 Michael H. Granof Award—the university’s top dissertation and graduate student award.
Underwritten by the University Co-op, the Granof Award is named in honor of Dr. Michael H. Granof, former chair of the Co-op board and longtime professor at the university. The winner of the Granof Award receives a $6,000 prize.

Piccirillo’s dissertation examines knots and four-dimensional spaces and resolves two well-known mathematical problems.
Already her work has garnered much attention in the field.
Piccirillo has given around 25 invited talks outside the university on her work. Following graduation, she begins a postdoctoral fellowship from the National Science Foundation at Brandeis University followed by the prestigious Moore Instructorship at the Massachusetts Institute of Technology.
“Lisa is an accomplished mathematician with already four papers to her credit that are or will be published in top journals in the field,” said her dissertation supervisor and mathematics Professor John Luecke in his nomination letter for the award. “[Her dissertation] gives a surprising, elegant argument answering an iconic, 50-year-old question.”
Piccirillo took time to answer some questions about her work.
How would you describe knot theory and four-dimensional topology to those outside the field?
If an ant living on the earth would like to leave an island without touching the water, it is going to have a hard time. Because on the 2-D surface of the Earth, the water completely surrounds the island. But, if the ant builds a bridge (which rises up, into a third dimension, above the water), then suddenly it has an option to leave the island. We naturally think about 3-D space all of the time. Studying 4-D space is fun because, just as the ant can leave the island once it's allowed to go up, in four dimensions more things are possible.
What drew you to this field?
I have always been drawn to spatial reasoning, and I like the creativity and challenge of trying to think carefully about objects that I can’t just draw a picture of.
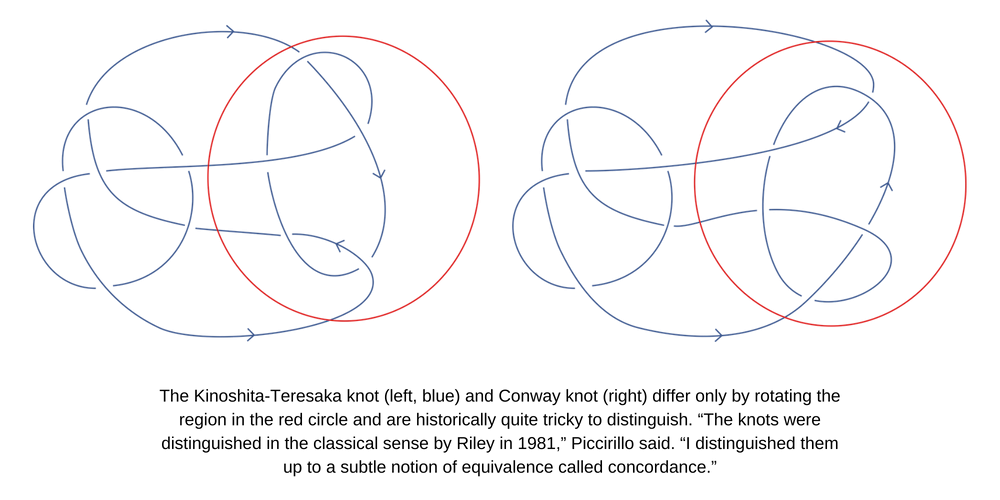
Your dissertation resolves two questions on well-known problems within the field: one from the Kirby Problem List and one first posed by John Conway. Why did you choose to examine these questions in particular?
When I was just starting research, I learned about the problem from the Kirby list and found it interesting, but presumably hard. Then, a few months later, someone solved a smaller case of it! That was very exciting and made me think that maybe the big problem was approachable with modern tools. That was pretty bold, but I enjoyed working on the problem so I was able to keep at it and eventually something worked. The Conway problem was serendipitous; someone mentioned the problem in a talk and I realized immediately that it should be approachable using the tools I study.
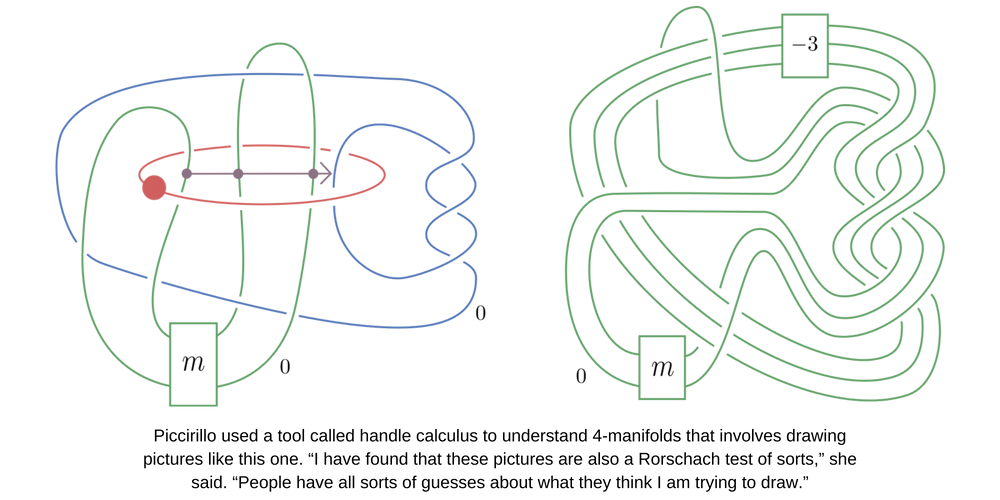
How did you go about addressing them? What was your methodology?
Well, it’s a bit technical? Maybe I can say something about how I choose my methodologies instead. Research is pretty hard, and 364 days a year you won’t solve anything. I’m not actually particularly disciplined, so to make up for this I work on problems where I find the things I am thinking about on the 364 unsuccessful days inherently interesting. Then it is fun and natural to work hard every day, and if you work hard and carefully for long enough I think you will probably solve your problem. I also worked on part of the Kirby problem with a collaborator who is a good friend and quite inspiring; that also makes working hard every day naturally rewarding.
What were your biggest challenges and how did you overcome them?
My biggest challenges were in college and early graduate school. I worried a lot about whether I would like math research and, even more so, whether I was smart enough to do math. This undermined both my ability to really engage with the community and my work. Slowly, eventually, I learned that I love math research (at least, I love three and four-manifold topology), and there is no such thing as smart-enough-to-do-math.
What is the importance of conducting research within this field?
There are lots of arguments about the importance of conducting basic research, like that you never know what useful things might fall out of it (I believe penicillin is the standard example), and because it provides the foundations for future applications. This latter is an especially strong motivation for research in mathematics.
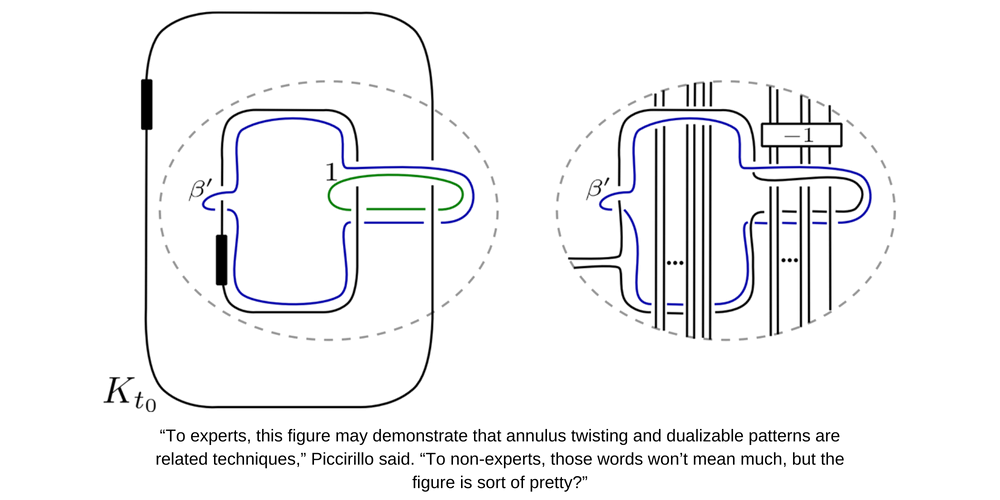
What role did your department play (whether faculty members or peers) in helping you with this research?
I think that you cannot overestimate the role that the topology group played in helping me with this research. When I was a young graduate student, I learned enormously from the older graduate students and postdocs. People were very open with their time and technical knowledge, but more importantly many people invested a lot of attention to developing seminars with a strong commitment to quality exposition and an inclusive and supportive community of people who work hard and support each other.
I still find these structures and cultures really helpful, but this was especially the case when I less technically proficient and more insecure. In addition, my advisor John Luecke was wildly gracious with his time and patience. I didn’t understand what it meant to understand something before I started trying to explain things to him. And I have benefitted hugely from conversations with Cameron Gordon, as well as from his leadership of this incredible research group. I’ll try not to go on and on, but it has been a privilege to be a part of this community, and I would have been far less successful without it.

